Introduction

If initially a set of N scattered data points in 3D are given and our
goal is to reconstruct a surface based on this data. Using CSRBF we create a spline implicit function f(x,y,z)=0 (surface) or
f(x,y,z)<=0 (volume).
There are two approaches to the reconstruction problem using RBF splines:
- Select initial carrier function (for example sphere) and compute the spline which will represent the deformation of initial carrier function. This approach leads to very smooth
surfaces, but requires quite a big radius of support R and thus computationally expensive. Also not all shapes are easy to reconstruct, because initial carrier function is not known for complex surfaces.
This approach was firstly proposed by V. Savchenko, A. Pasko, O. Okunev and T. Kunii, Function representation of solids reconstructed from scattered surface points and contours, Computer Graphics Forum, 14(4), 181-188, 1995.
- "Both-sides" approach proposed by G. Turk and J. F. O`Brien, Shape Transformation Using Variational Implicit Functions, SIGGRAPH`99, 335-342, 1999.
doubles the number of points by selecting two points on both sides of normal for each point from initial dataset and sets the right part to +1 or -1 depending on the side of normal. As RBF functions are continous it means that they will turn to 0 somwehere near to the initial point and the sharpness of the surface defined in this way will depend on the distance between points taken on normals. This approach creates sharp surfaces of any geometry in reasonable time (because we can select a small radius of support R), but the problem of finding normals is itself difficult.
In practice, the problem of reconstruction with RBFs consists of the following steps: sorting the data, constructing the system of linear algebraic equations (SLAE), solving the SLAE, and evaluating the functions. In fact, while the solution of the system is the limiting step, constructing the matrix and evaluating the functions to extract the isosurface may also be computationally expensive.
We use CSRBF splines instead of RBF for both approaches which leads to a sparce matrix of size N+4*N+4 in SLAE. We have created a special algorithm based on octal tree subdivision of the intial space, which sorts initial data points in such a way that the resulting matrix is band-diagonal, which enables us to store it very compactly and solve it by using fast and easy direct solver. Later the octal tree is also used
in the process of the surface extraction to accelerate the computation of the implicit function f(x,y,z).
Documents
- Octal tree based library description : You can download (pdf, 122Kib) a short descrption of our algorithms and software library.
Examples (sphere as a carrier function)
- Seashell reconstruction :
Model of the Sea shell. You can download source
normalized point data (26 KiB) of this model and the result of reconstruction
model in vtk file format (321 KiB).
 |
Test configuration: AMD Athlon 1000 Mhz, 128 MB RAM,
Microsoft Windows 2000.
| Number of points - N |
915 (model of the seashell) |
| Max. number of points in the leaf - K |
10 |
| Tree creation (inc. file reading time) |
291 nodes at 8 levels. 0.001 sec. |
| Selected radius r |
0.2 |
| Sorting time┬а |
0.03 sec. |
| Matrix calculation time |
0.02 sec. |
| Memory requirement to store the band diagonal sub-matrix of the matrix
A |
669068 bytes (0 MiB) (if stored traditionally it would be 3348900
bytes (3 MiB)) |
| Solution time by Cholesky decomposition |
0.1 sec. |
| Rendering time |
0.41 sec. |
|
- Human head reconstruction :
Model of the Human Head. You can download source
normalized point data (41 KiB) of this model and the result of reconstruction
model in vtk file format (293 KiB).
 |
Test configuration: AMD Athlon 1000 Mhz, 128 MB RAM,
Microsoft Windows 2000.
| Number of points - N |
1487 (model of the head) |
| Max. number of points in the leaf - K |
10 |
| Tree creation (inc. file reading time) |
467 nodes at 6 levels. 0.001 sec. |
| Selected radius r |
0.2 |
| Sorting time |
0.03 sec. |
| Matrix calculation time |
0.05 sec. |
| Memory requirement to store the band diagonal sub-matrix of the matrix
A |
1675800 bytes (1 MiB) (if stored traditionally it would be 8856576
bytes (8 MiB)) |
| Solution time by Cholesky decomposition |
0.911 sec. |
| Rendering time |
0.491 sec. |
|
Examples (both-sides approach)
- Lion-dog :
|
|
|
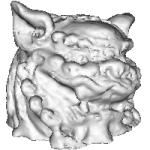
(a) Reconstruction of the тАЬLion-dogтАЭ model (courtesy of Dr. A. Belyaev of The University of Aizu) from 19125 points; a sphere as a тАЬcarrier functionтАЭ is used, r = 0.3. Reconstruction is very slow (about 38 min), due to a big radius of support, but the result looks visually smooth,
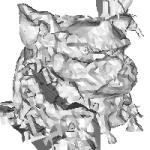
| | (b) Reconstruction based on PhD work of Hugues Hoppe, |
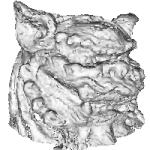
(c)The data taken from the model of lion-dog (d)(courtesy of Dr. A. Belyaev of The University of Aizu) contains 355586 source points which leads to 71172 points taken on both sides of normal. You can download source normalized point data (1.98 MiB) of this model and the result of reconstruction model in vtk file format (12.94 MiB).
Processing time on our test configuration (AMD Athlon 1000 Mhz, 128 MB RAM, Microsoft Windows 2000):
| Radius R | 0.01 |
| Tree build time | 0.04 sec. |
| Sorting time | 1.482 sec. |
| Constructing time | 1.312 sec. |
| Compact size of matrix A is (71172*71172) | 36598952 bytes (34 MiB) <= 3081945152 bytes (2939 MiB) if stored as full matrix. |
| Solving time | 7.721 sec. |
| Rendering time | 5.127 sec. |
| | (d) source data points. |
|
Demo software
- Online reconstuction server :
Donwload some of our test files and save them to disk or prepear some of your own examples. Note that the data you upload should be already normalized, i.e. all point should lie in unit cube 0-1,0-1,0-1. File format is following:
Normalized points for use with sphere as a carrier function:
xmin xmax ymin ymax zmin zmax
xi yi zi
...
(first line defines the original model bounds,
before the normalization.)
Normalized file for both-sides approach:
xmin xmax ymin ymax zmin zmax
xi+ yi+ zi+ xi- yi- zi-
...
(first line defines the original model bounds,
before the normalization, all other lines defines points on + side and - side of normals).
You'll also need a VRML plug-in for your browser, we reccomend Cortona http://www.parallelgraphics.com/products/cortona/download/.
Now you can appload file and see it as a VRML object. We strongly recommend you to use Netscape Communicator 4.x browser. Be prepared to wait for some time, network may be quite busy.
- Surface reconstruction :
Note:This program was compiled for Microsoft Windows and can be used on any PC with Microsoft Windows 9x, Me, NT, 2000 or XP installed. Before running this program you need to download and install VTK runtime library VTK Core (2.8 MiB), if you have not done it already.
Normalizer: performs automatic normalization of source point data, given *.pts file:
xi yi zi
...
it creates a normalized point data file (*.npts) for use with our reconstruction software.
Usage: normalizer.exe file.pts file.npts
NormalizerNorm: performs automatic normalization of source point data taken on both sides of normals, given *.pts file:
xi- yi- zi- xi+ yi+ zi+
...
it creates a normalized point data file (*.npts) for use with our reconstruction software.
Usage: normalizernorm.exe file.pts file.npts
Reconstruction: performs automatic reconstruction of normalized source point data, given *.npts file and selected radius of support r. If the file contains normalized points taken on the both sides of normal the programm will use both-sides approach, if not it will use sphere as initial carrier function. The model will be rendered on screen and also saved on disk in vtk file format (reconstructed_shape.vtk).
Usage: reconstruction.exe file.npts 0.28
Download: exe, 156 KiB.
Download example data (all examples): exe, 4.7 MiB.